用Python形象地解决酒缸分酒问题

最近遇到一个有意思的题目，看上去不相关的两个事物有着同样的转移状态，并且设定规则后过程可以用程序模拟出来，遂记之。

问题提出

你有一个8升的酒坛，里面装满了酒，另外还有两个分别是5升和3升的空酒坛，3个酒坛都没有刻度，现在需要倒出正好4升的酒，需要怎么操作？

从题目来看，我们需要把3个缸的酒倒来倒去，直到某个酒缸里面是4升酒。这个问题的解法很有趣，我们假设能装5升酒的坛子叫A，3升的坛子是B，8升的坛子是C，开始的时候我们可以先在A坛子里装满酒也可以先在B坛子装满酒（只装一部分我们是没办法知道是多少升的，没有用）。
假设先给A装满酒，那么A,B坛子的状态就是(5,0)，表示这时候是A有5升酒，B有0升，这时候可以的做法是把A中的酒倒到B里，变成(2,3)，也可以从C倒3升到B，变成(5,3)，但这种情况下一步只能把A或B中的酒倒回C，回到开始状态了；第三种情况是把A中的酒倒进C里，变成(0,0)，更加没意义了。

一个3种倒酒情况的图

台球解法

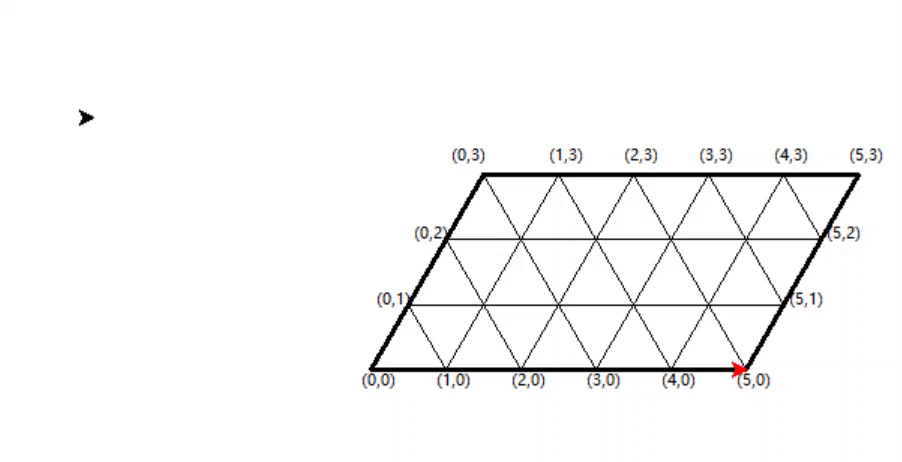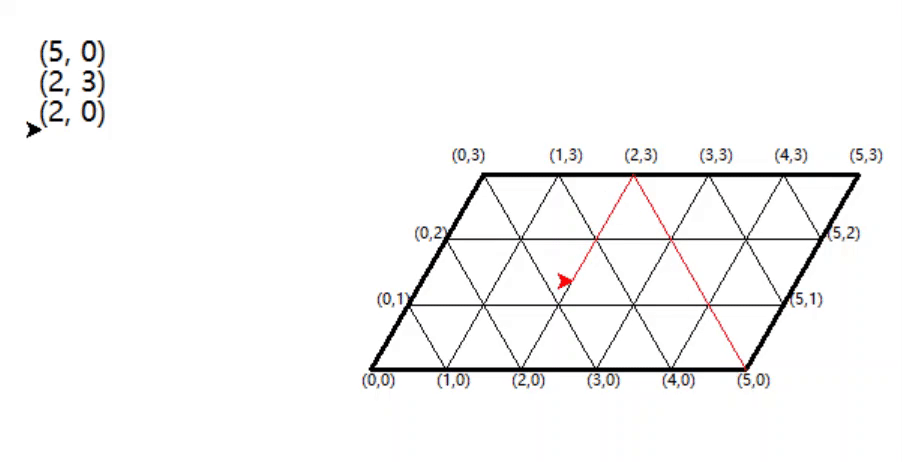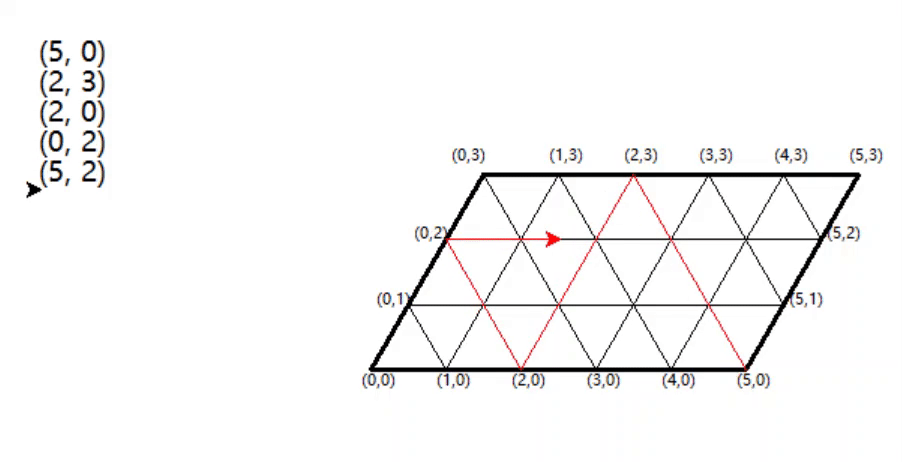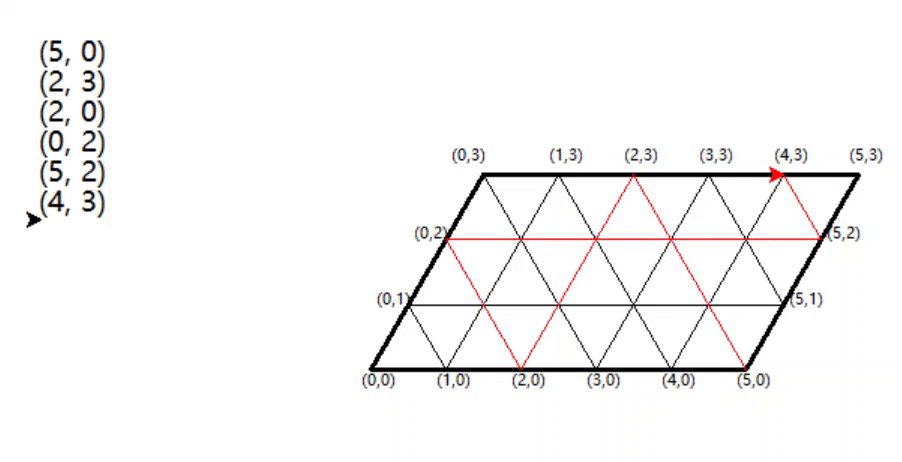
于是有效做法是从(5,0)状态变成(2,3)状态，我们可以想象一个菱形的台球桌，从一个地方发球，球经过和桌子边缘的碰撞有一个弹射的路径。来看一下一个从(5,0)出发的球，在一个5 x 3的台球桌上，沿三角形边线方向撞击台球，其路径会是(2,3) (2,0) (0,2) (5,2) (4,3)
如下图

我们之前把(5,0)理解为A坛有5升酒，B坛有0升，那么从(5,0)到(2,3)到(2,0)就可以理解为这两个酒坛里面液体的量的变化，也就是酒坛里的状态转移路径。

具体就是从A倒酒进B里，直到B满了（变成(2,3)），再把B里的酒倒到C里，变成(2,0)，把B中剩余的2升倒到C里，变成(0,2),这时候把B倒满，变成(5,2)，B可以装3升，目前是2升，所以从A倒酒进B里，B原来是2升，倒满就是从A倒出了1升，所以A是4升，也就是(4,3)，达到要求，

实际中解这类题我们可以画x*y的菱形手动画路径，但我们可以用程序模拟这一过程，下面用Python实现一下。

python 模拟

可以通过计算方向和用反射定律去模拟球的轨迹，也可以取巧只通过路径去模拟轨迹。
首先这个台球桌是菱形的，出发点在(5,0)或(0,3) （都能得到结果），我们从路径上看，(5,0)只有一个路径可以走，而(2,3)有两条路可以走，分别到达(2,0)或者(5,0)，在(0,0)以及(5,3)这两个点是没有路径的，

我们再分析路径的规律，x横坐标的最大值，y是纵坐标最大值，设n球在横坐标的位置，m为在纵坐标上的位置，对于点设n球在横坐标的位置，m为在纵坐标上的位置，对于点(n,0)，n不等于0和不等于x时，都有两条路，且从一条路过来必然下一步要走另一条路，这两条路的规律是(n,y)以及(0,n)，当n大于y时，到不了(0,n)，只能到(n-y,y)；根据这些规律模拟出边界上各个顶点对应的路，代码如下：

t=8
e=4
x,y=5,3
if y>x:
    x,y=y,x #保证x>y
#从路径来看，一个点要么没有路径，要么有1条路径，要么2条，没有其他情况；
#0条对应：(0,0) & (x,y)
#1条：(x,0) & (0,y)
#2条：(n,m) 0<n<x   0<m<y
r={}
r[(0,0)]=[]
r[(x,y)]=[]
r[(x,0)]=[(x-y,y)]
r[(0,y)]=[(y,0)]
for n in range(1,x):
    if n<y:
        r[(n,0)]=[(0,n),(n,y)]
    else:
        r[(n,0)]=[(n-y,y),(n,y)]
    k=n+y
    if k>x:
        r[(n,y)]=[(n,0),(x,n+y-x)]
    else:
        r[(n,y)]=[(n,0),(n+y,0)]
for m in range(1,y):
    #m必然要小于x if m<x:  不需要
    r[(0,m)]=[(m,0),(x,m)]
    r[(x,m)]=[(0,m),(x+m-y,y)]

我们就可以从一个点(5,0)出发，看具体的效果：

w=[x,0]  #上一个点
s=[x,0]
plst=[s] #开始
while s[0]!=e and s[1]!=e:
    ss=(s[0],s[1])
    sw=r[ss]
    slen=len(sw)
    
    if slen==1:
        w=s.copy()
        s[0]=sw[0][0]
        s[1]=sw[0][1]
    elif slen==2:
        if sw[0][0]==w[0] and sw[0][1]==w[1]:
            w=s.copy()
            s[0]=sw[1][0]
            s[1]=sw[1][1]
        elif sw[1][0]==w[0] and sw[1][1]==w[1]:
            w=s.copy()
            s[0]=sw[0][0]
            s[1]=sw[0][1]
        else:
            print(s,sw,slen)
    else:
        print(s,sw,slen)
    plst.append(s)

print(plst)

当x=5，y=3时，以上代码输出[[5,0], [2,3], [2,0], [0,2], [5,2], [4,3]]，代表A，B两个酒缸之内各有多少酒。

利用turtle可视化

路径我们可以通过上面的代码算出来，从而得到这题的结果，但不够形象，我们通过Python的turtle库把这一过程画出来，turtle是Python内置的一个画图库，通过goto、left、right等命令控制一个小海龟（turtle）在画布（canvas）上爬行，从而得到各种图案，可以拿来绘制分形图案、小猪佩奇等。这次的模拟路径可视化也可以用pygame库。

正常的画布是一个直角坐标系，我们这里需要一个纵轴和横轴之间是60度的斜坐标系，因此通过以下函数转换：

1 2	def drawToXY(x,y,turtle=turtle,sin=sin,pc=50): #sin=sin(60°)=sqrt(3)/2; pc转换因子 turtle.goto(xpc+0.5ypc,pcsin*y) #直角坐标转斜坐标

通过drawToXY()我们可以很方便地绘制出台球桌的外框：

def drawDiamond(x,y,turtle=turtle,pc=pc,sin=sin):  #画边界
	turtle.pensize(3) #占3个像素的笔宽
	drawToXY(x,0,turtle,sin)
	drawToXY(x,y,turtle,sin)
	drawToXY(0,y,turtle,sin)
	drawToXY(0,0,turtle,sin)  #外框
	turtle.pensize(1) #默认笔宽

绘制一个5 x 3的外框效果如下：

绘制外框之后再加上内部点的连接，就像把一个(X,Y)的方格变形为菱形，并加上边界坐标，在turtle上写文本通过语句turtle.write(txt, font=( "微软雅黑", size, "normal"))实现。

之后便可以绘制从(5,0)出发的球的路径了：

def drawPlst(plst,turtle=turtle,t2=t2):
	dt=25
	dy=200
	k=0
	for p in plst:
		drawText(-180,dy-k*dt,str(p),t2,size=14) #在另一侧写下经过的边界点
		drawToXY(p[0],p[1],t1)
		k+=1

def drawText(x,y,txt,turtle=turtle,size=14):
	turtle.penup()
	turtle.goto(x,y)
	turtle.pendown()
	turtle.write(txt, font=("微软雅黑", size, "normal"))
plst=plst=[(5,0),(2,3),(2,0),(0,2),(5,2),(4,3)]
t1.color("red")
#t1.speed(2) #绘制速度，[0,10] 数值越大速度越快
drawPlst(plst,t1,t2)

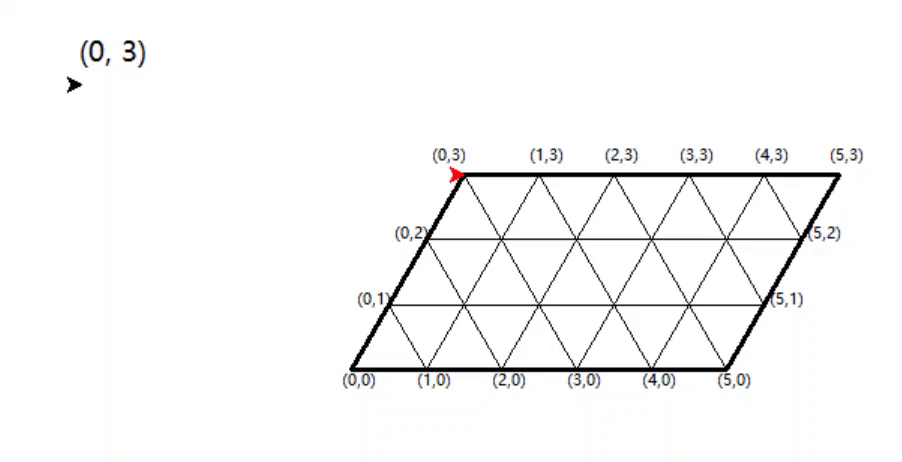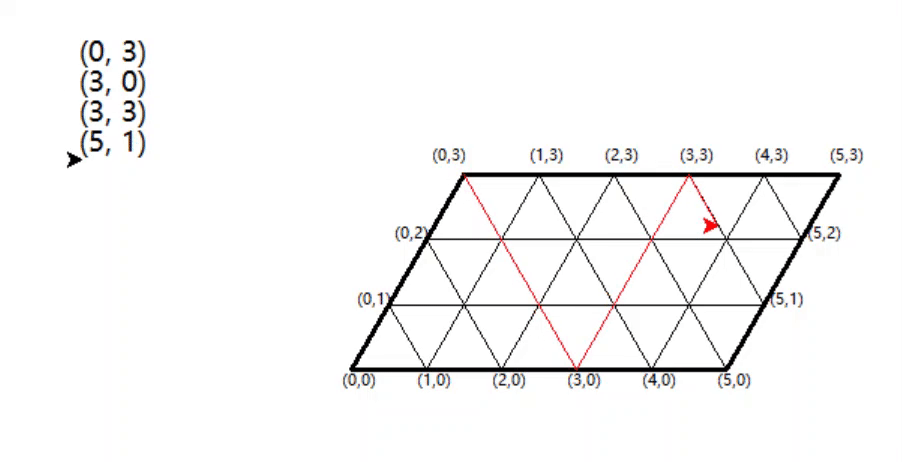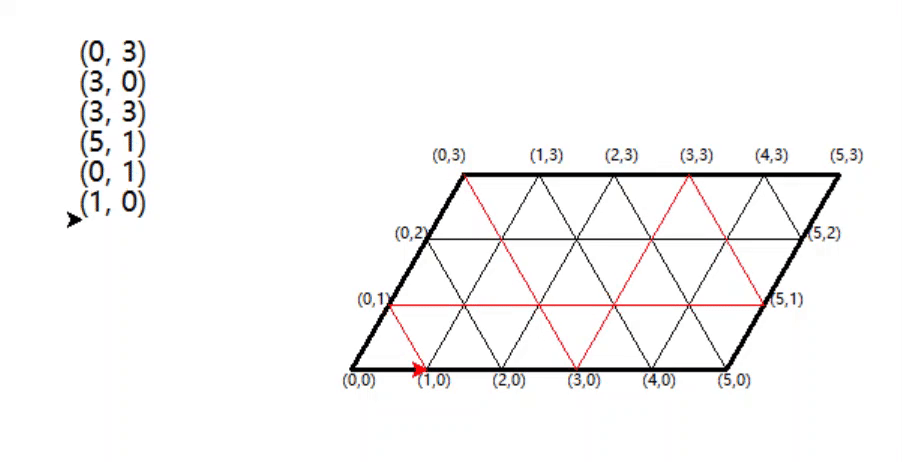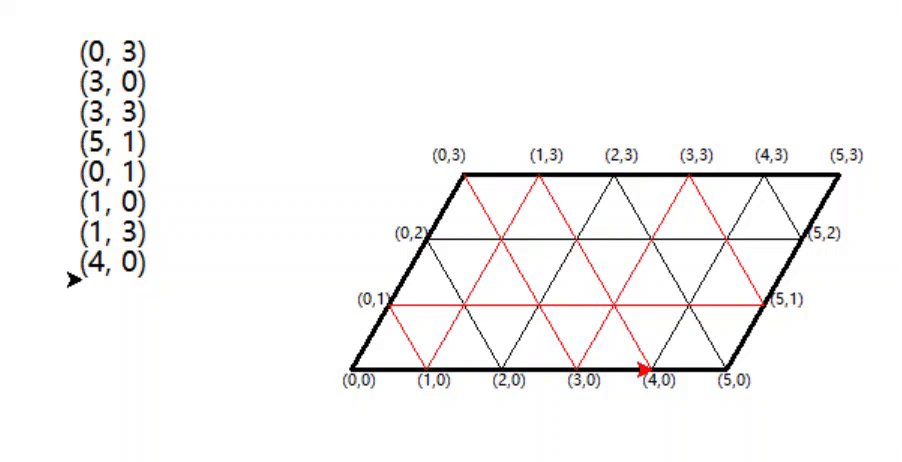
从(0,3)出发的效果：

一个类似的题

我们在河边分别有一个7升的水桶和5升的水桶，都没有刻度，如何用最少的次数装6升的水出来

分析一下我们知道，最少次数的方式就是我们台球路径的做法，之前我们对酒缸C的处理和一条容量无限的河本质是一样的。

所以这题的解法用程序模拟效果如下图：